S prenovljenim učnim načrtom so se vzorcem na široko odprla vrata v pouk matematike. Učenci vzorce prepoznavajo, nadaljujejo, izpeljujejo posplošitve – verbalno in simbolno. V prispevku so predstavljeni nekateri vzorci, ki se pojavljajo na različnih stopnjah osnovnošolskega izobraževanja.

V vsakdanjem življenju lahko najdemo vzorce v različnih pojavnih oblikah (ciklično menjavanje letnih časov, izmenjevanje svetlega in temnega dela dneva, ritmične pesmi in plesi, vzorci na oblačilih, fasadah stavb …). Z vsemi se otrok seznani že v predšolskem obdobju.

Nizanje perlic na vrvic

Glasba in ritmično gibanje (Vir: Shutterstock)

Vzorci na fasadi (Vir: Shutterstock)

Vzorci v prvi triadi

Vzorce se začne sistematično obravnavati že v prvem razredu. V učnem načrtu so opredeljeni z dvema ciljema, ki se ponovita še v drugem in tretjem razredu.

Učenci naj bi:

1. oblikovali slikovne in geometrijske vzorce,
2. prepoznali pravilo v slikovnem in geometrijskem vzorcu in vzorec nadaljevali.

V didaktičnih priporočilih učnega načrta je zapisano še, da naj bi učenci na tej stopnji že ugotovili, da je barvni vzorec rdeče-rdeče-modro-rdeče-rdeče-modro vzorec z enakim »pravilom« kot glasovni vzorec ko-ko-dak-ko-ko-dak. Na ta način učence že v zgodnjih letih izobraževanja uvedemo v algebro. Prvi koraki temeljijo na ugotovitvi, da lahko zapisana vzorca opišemo kot AABAAB.

Ker učni načrt ne predpisuje stopnjevanja učne vsebine, moramo biti pri pouku toliko bolj previdni, da se obravnava po težavnosti kljub temu stopnjuje. Zato v prvem razredu običajno obravnavamo najpreprostejši vzorec ABAB.

Vzorce sestavljamo z:

• najrazličnejšim nestrukturiranim materialom:
  • drevesnimi listi,
  • plodovi,
  • sponkami,
  • gumbi;
• pa tudi z geometrijskimi telesi, liki,
• s številkami in črkami.

Vzorce gradimo v vse smeri, vodoravno, navpično, poševno, od leve proti desni, v vrstice, v stolpce …

Vzorec ABAB z drevesnimi listi, od leve proti desni

Vzorec ABBABB s sponkami, nadaljevanje v obe smeri

Vzorec ABCABC s stolpcem iz kock

V učbeniških gradivih se največkrat pojavijo v obliki izmeničnega barvanja, risanja likov ali zapisovanja črk oz. številk.

Učbenik Lili in Bine, SDZ za matematiko, 1. del, str. 12

Učbenik En dva tri, odkrij jo ti, 1. del str. 56

Učbenik En dva tri, odkrij jo ti, 1. del str. 33

Vzorci v drugi triadi

V drugi triadi se cilja iz prve triade tako rekoč ponovita. V didaktičnih priporočilih pa je omenjeno, da naj »učenci oblikujejo simetrične oblike in vzorce s premiki, vrteži ter z zrcaljenjem«. Primer takega oblikovanja vzorca je:

►▼▲◄ ►▼▲◄

Na tej stopnji poskušamo od učencev že dobiti ubeseditev pravila. Seznanijo se tudi z osnovnim besediščem (osnovni motiv oz. gradnik vzorca, člen vzorca, vzporedni premik, zrcaljenje in vrtež).

V šestem razredu učenci že »v mislih« nadaljujejo vzorce z več členi, kot jih lahko sestavijo oz. narišejo, ter poskušajo ugotoviti, kateri del osnovnega motiva stoji npr. na 20. mestu vzorca. Pri tem si pomagajo z matematičnimi pravili, formulami … (UN, str. 39).

Uporabljamo tudi t. i. »naraščajoče« vzorce.

Učbenik Svet števil in oblik 7, str. 100

Učbenik Kocka 6, str. 74

Vzorci v tretji triadi

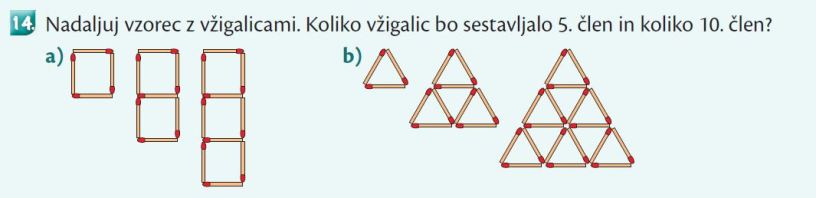
V 7. razredu se učenci učijo posploševanja in zapisovanja algebrskih izrazov. Uporabijo pridobljeno znanje o vzorcih in ga nadgradijo. »Učenci opazujejo vzorce, ugotovijo pravilo in ga zapišejo z algebrskim izrazom. Primer: Koliko vžigalic bi potrebovali za 10. lik (za 7. razred) in koliko vžigalic za n-ti lik (8. razred)?« (UN, str. 56

Že angleški matematik Hardy je leta 1940 primerjal matematike s slikarji in pesniki, ki v svojih umetninah ustvarjajo vzorce, le da so vzorci matematikov trajnejši, zgrajeni iz idej. Morda je matematika prav zaradi tega postala tako uspešna in prepletena z drugimi vejami znanosti, navsezadnje jih kot merilo inteligence uporabljajo tudi psihologi.

Priloga: učni list

Avtorica prispevka: Simona Knez