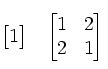SUDOKU – NEREŠLJIV MATEMATIČNI PROBLEM?
Leta 1986 je japonska ugankarska revija Nikoli Co Ltd. začela objavljati logične uganke, ki so obnorele svet. Najbolj zanimivo je, da korenine igre segajo v 18. stoletje in da jo danes v šolah priporočajo učencem za razvijanje logičnih spretnosti, le redki pa se zavedajo, da je sudoku primer še nerešenega problema, ki ga skušajo razvozlati najslavnejši matematiki.
SLIKA 1
Sudoku je latinski kvadrat
Sudoku je poseben primer latinskega kvadrata reda 9 x 9. Latinski kvadrat reda n x n je kvadratna shema, v kateri nastopijo števila od 1 do n v vsaki vrstici in v vsakem stolpcu natanko enkrat. Latinski kvadrati so lahko različnih redov od 1 naprej. Prvi se je z njimi resno ukvarjal eden največjih matematičnih genijev Leonhard Euler in jim tudi dal ime.
Slika 2: Leonhard Euler (1707–1783)
Slika 3: Latinskemu kvadratu zelo podobno shemo so našli napisano na steni kopališča v vili bogatega rimskega meščana v zasutih Pompejih. Besedilo je zanimivo, ker nosi jasno sporočilo: »Sejalec Arepo pri delu drži plug«, ki ga lahko beremo enako v štirih smereh (vodoravno in navpično).
Slika 4: Elementi latinskega kvadrata so lahko tudi črke in drugi simboli, pa tudi barve in vzorci.
Sudoku rešujemo s kombinatoriko
Za izračun števila različnih latinskih kvadratov posameznega reda potrebujemo precej logičnega sklepanja ali pa nekaj znanja kombinatorike.
Očitno je latinski kvadrat reda 1 le eden, tudi pri redu 2 ni težav – obstajata dva različna, pri redu 3 pa je že nekaj več dela.
Slika 5
Sudoku – kako se ga lotiti?
Zamislimo si prazno razpredelnico kvadratne oblike 3 x 3. V posamezna polja moramo razvrstiti števila od 1 do 3 tako, da nastopijo vsa tri v vsaki vrstici in v vsakem stolpcu natanko po enkrat.
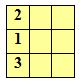
Denimo, da začnemo z najvišjim poljem prvega stolpca: vanj lahko razporedimo eno od treh števk – zato imamo tri možnosti. V spodnje polje lahko razvrstimo eno od ostalih dveh števk, imamo torej dve možnosti; za zadnje polje stolpca nam ostane ena števka. Po osnovnem izreku kombinatorike je vseh razporedov toliko, kolikor je razvrstitev ali permutacij treh števil, to pa je P3 = 3! = 3 · 2 · 1 = 6. Eno od teh šestih možnosti kaže slika 6.
Slika 6
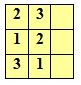
Za izpolnitev zgornjega polja drugega stolpca imamo zaradi zahteve igre na razpolago le dve števki; recimo, da izberemo 3; v drugo polje moramo postaviti števko, ki ni 3 in 1 – zato je lahko le 2; v spodnje polje moramo postaviti 1. Možnosti za drugi stolpec sta tako le dve.
Slika 7
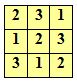
Števke zadnjega stolpca so natančno določene že s pravili igre.
Slika 8
Spet se spomnimo osnovnega izreka kombinatorike in vidimo, da je število možnosti za zapolnitev latinskega kvadrata 3 x 3 enako 12.
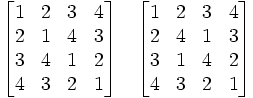
Vseh latinskih kvadratov reda 4 x 4 je kar 576, dva od njih pa sta posebnega pomena za abstraktno algebro, vejo matematike, ki se je začela razvijati v 19. stoletju.
Razvrstitev števil v omenjenih dveh latinskih kvadratih definirata dve dvočleni operaciji elementov množice , ki jima po zgledu množenja s števili rečemo kar »poštevanki«. Lastnosti obeh operacij lahko preberemo iz posamezne tabele.
Slika 9 (a, b)
Slika 10: Norveški matematik Niels Henrik Abel (1802–1829)
Kleinov četverček
Množica z operacijo iz prvega kvadrata se imenuje Kleinov četverček in pomeni Abelovo grupo – množico s posebno strukturo, ki zadošča naslednjim zahtevam:
- Operacija je notranja: »produkt« katerih koli dveh elementov je spet element množice.
- V množici obstaja nevtralni element, podobno kot bi v množici celih števil množili z 1.
- Vsakemu elementu lahko najdemo natanko en inverzni element, ki pri množenju z njim da nevtralni element.
- Operacija je komutativna oz. vrstni red elementov v operaciji ni pomemben.
O zgornjih zahtevah se za Kleinov četverček ni težko prepričati:
- Prva zahteva je očitno izpolnjena – v tabeli so le elementi od 1 do 4.
- Nevtralni element je 1.
- Vsak element je inverzen samemu sebi: , , , .
- Komutativnost lahko vidimo iz simetričnosti tabele glede na glavno diagonalo.
Ciklični četverček
Zelo podobno lahko ugotovimo, da je ista množica pri operaciji »množenja po modulu 5«, ko števili običajno zmnožimo in od produkta odštejemo mnogokratnik števila 5, da je rezultat število od 0 do 4, tudi Abelova grupa z imenom »ciklični četverček« (drugi kvadrat na sliki 9). Nevtralni element je spet 1, inverzni elementi zapored pa so 1, 3, 2, 4 (1 in 4 sta inverzna sama sebi, 2 in 3 pa drug drugemu). Zaradi komutativnosti je tudi ta tabela simetrična glede na glavno diagonalo.
Na pogled in po imenu abstraktna matematika latinskih kvadratov se je kasneje izkazala za zelo uporabno tudi v drugih znanostih, predvsem pri raziskavah molekularne simetrije in pri spektroskopiji.
USTVARITE NOVO ZNANJE – SPOZNAJTE NAJBOLJ MODRE WEBINARJE
Aktualne izobraževalne teme v obliki krajših spletnih izobraževanj so že na voljo! Pridobite kompetence prihodnosti, znanja in veščine, ki pedagoškim in strokovnim delavcem omogočajo strokovno in osebno rast.
Kako rešujemo sudoku?
Pravila reševanja uganke sudoku so preprosta: v kvadratno razpredelnico, ki ima 9 x 9 polj in je sestavljena iz devetih kvadratnih razpredelnic s po 3 x 3 polji, med katerimi so nekatera izpolnjena s števkami – to so podatki – druga pa prazna, je treba vstaviti števke od 1 do 9 tako, da je vsaka od razpredelnic 3 x 3 latinski kvadrat in da je tudi celotna razpredelnica 9 x 9 latinski kvadrat – to pomeni, da v vsaki vrstici in v vsakem stolpcu nastopajo vse različne števke od 1 do 9. Pri tem za števke ne veljajo nobene aritmetične zakonitosti in jih lahko nadomestimo s črkami, drugimi simboli ali celo z barvami.
Čeprav so pravila preprosta, reševanje zahteva precej kombinatoričnih spretnosti. Uganke so razvrščene po težavnosti – v preproste, srednje težke in težke.
Sudoku v matematiki
Pojav igre sudoku se je dotaknil tudi matematikov znanstvenikov. Ugotovili so, da je teoretično iskanje števila rešitev igre sudoku NP-problem. Za osvetlitev najprej poglejmo nekaj ozadja.
Za reševanje problemov matematiki uporabljajo postopke, ki se imenujejo algoritmi. Včasih algoritem teoretično obstaja, v praksi pa ni uporaben. Preprost primer takega algoritma je Eratostenovo sito za iskanje praštevil. Naravno število, za katero ne vemo, ali je praštevilo ali sestavljeno število, moramo po vrsti deliti z vsemi števili, ki so manjša od , in ugotoviti morebitno deljivost ali nedeljivost.
Na pogled zelo preprosto, v praksi pa neizvedljivo, saj bi za testiranje petdesetmestnega števila izredno učinkovit računalniški program potreboval (verjeli ali ne!) deset milijard let. Navedeni primer je zelo sodoben, saj v kriptografiji (tajnopisju) danes uporabljajo praštevila, ki imajo od 70 do 100 mest.
Učinkovitost algoritma pri reševanju sudokuja
Poleg obstoja algoritma je torej zelo pomembna tudi njegova učinkovitost; slednjo merijo s številom korakov, ki jih za rešitev problema naredi t. i. Turingov stroj. To je hipotetična računska naprava, sestavljena iz glave in neskončnega celičnega traku. Glava Turingovega stroja lahko naenkrat s traku prebere znak ali ga nanj napiše. Celice na traku so lahko prazne ali pa vsebujejo znak neke »abecede« – najpreprostejša je kar tista z znakoma 0 in 1 (glava je v vsakem trenutku v enem od teh dveh stanj).
Delovanje stroja poteka zaporedno po korakih, vsak korak pa je sestavljen iz treh različnih dejanj. Glava vsakokrat pregleda celico na traku, in naslednji opravek je odvisen prav od vsebine te celice in stanja stroja. Glede na ta dva podatka stroj zbriše obstoječi znak in pusti presledek ali pa zapiše nov znak (ki je lahko enak zbrisanemu). Nato stroj premakne trak v eno ali drugo smer.
Obnašanje stroja je tako določeno z množico navodil, ki za vsako stanje in vsak prebrani simbol predpisujejo, katera tri dejanja se morajo izvesti. To zaporedje navodil se imenuje tudi algoritem.
Slika 11: Alan Turing (1912–1954)
Polinomski in eksponentni algoritmi
Algoritem je polinomski oz. teče v polinomskem času, če je za reševanje naloge z vhodnimi podatki dolžine n potrebnih manj kot korakov in sta C in k isti naravni števili za vsak n.
Algoritmi, ki ne tečejo v polinomskem času, so eksponentni. Najbrž je že jasno, da so učinkoviti le polinomski algoritmi, eksponentni pa so zaradi prevelike časovne zahtevnosti neučinkoviti.
Od vseh se danes najbolj ukvarjajo z NP-polnimi problemi: ti so eksponentni, da pa se to dokazati v polinomskem času.
Nedeterministični polinomski čas
Najslavnejši NP-problemi (kratica pomeni nedeterministični polinomski čas) so:
- Problem trgovskega potnika: Trgovski potnik mora obhoditi večje število (npr. n > 50) različnih krajev. Izbrati je treba tisti vrstni red, pri katerem bo prepotovana razdalja najkrajša.
- Problem Hamiltonovega cikla: Množica krajev je povezana s cestnim omrežjem. Ali obstaja obhod, pri katerem vsak kraj obiščemo natanko enkrat in se vrnemo v izhodiščno točko?
- Barvanje zemljevida: Ali je mogoče dani zemljevid pobarvati s tremi barvami tako, da sta sosednji državi obarvani z različnima barvama?
- Razvrščanje poslov na več procesorjih: Imamo množico poslov in množico procesorjev in za vsak posel vemo, koliko časa bi tekel na posameznem procesorju. Procesorji delajo paralelno, obdelava poslov na posameznem procesorju pa zaporedno. Ali je mogoče posle razporediti na procesorje tako, da bo celotna obdelava zahtevala določeno vnaprej znano število (ali celo manj) časovnih enot?
Za naštete naloge, pa tudi za rešitve igre sudoku višjega reda še niso našli učinkovitih algoritmov, in vse kaže, da najbrž sploh ne obstajajo.
Avtor: Gregor Pavlič