VERJETNOSTNI RAČUN
Pravilno geometrijsko telo heksaeder z rahlo obrušenimi ogli in z naslikanimi pikami je v zgodovini ljudem prineslo veliko užitka, pa tudi veliko gorja. Marsikdo je v igralni vročici stavil vse in – dobil ali izgubil. Igralna kocka je v 16. stoletju postala tudi predmet preučevanja matematikov in porodila novo matematično disciplino – verjetnostni račun.
Verjetnostni račun skozi zgodovino
Iznajdba igralne kocke je zavita v skrivnost, kar ni čudno, saj naj bi jo poznali in se z njo zabavali že pred več kot 5000 leti. Res še ni imela natančno take oblike kot danes, imela pa je isto funkcijo. Najstarejši predhodniki današnjih igralnih kock so astragaliji: drobne gleženjske kosti dvoprstih kopitarjev. Te kosti imajo šest stranskih ploskev, od katerih so štiri ravne, in so po vsej verjetnosti služile za igro. Astragalije so uporabljali stari Egipčani že 3500 let pr. Kr. Najpogosteje so uporabljali ovčje kosti, najbolj cenjene pa so bile kosti antilope.
Po Platonu naj bi kocko iznašli bogovi, natančneje, egipčansko božanstvo Teuta. Spet po drugi razlagi naj bi jo iznašel Palamed, grški junak pred Trojo, ki je bil znan po izredni bistroumnosti. Njegovi vojaki naj bi si med obleganjem Troje krajšali čas z »metanjem kosti«. Grški zgodovinar Herodot pripisuje iznajdbo praktičnim Lidijcem, ki so z igro blažili hudo lakoto: vsak drugi dan so jedli, vmes pa so kockali.
SLIKA 1: Grška vojaka pri igri
Verjetnostni račun in Rimljani
Igre na srečo so poznali tudi stari Rimljani. Pri izkopavanjih v tragično zasutih Pompejih in Herkulaneumu so namreč našli tudi igralne kocke. Rimski cesarji Avgust, Komod, Kaligula in Neron so bili prav obsedeni s kockanjem. Klavdij, strasten hazarder, je o tej igri celo napisal razpravo, ki pa se ni ohranila. Bil je tako zasvojen, da je imel na svojem potovalnem vozu posebno vgrajeno mizo, ki je omogočala igranje tudi na najslabših poteh. V eni sami igri je bil sposoben staviti tudi bajnih 400 000 sestercev.
SLIKA 2: Stenska slika prikazuje Rimljanke pri kockanju z astragalijem
Uporaba verjetnostnega računa pri kockanju
Iz zgodovinskih poročil je vidno, da so kocko poleg preprostih ljudi z veseljem metali tudi vladarji. Norveški kralj Olaf Haraldsson je v 11. stoletju na kocko postavil kar celo kraljestvo, v času francoskega kralja Henrika IV. pa je ta zabava dobesedno obnorela dvor.
Sčasoma so se pri tej igri pojavile tudi goljufije oz. obtežene kocke, zato je bilo kockanje v 16. stoletju kar sinonim za goljufanje. Leta 1545 je izšla razprava Toxophilus, v kateri je avtor Roger Ascham naštel in opisal vse mogoče načine goljufanja pri kockanju.
Slika 3 prikazuje nekatere od 24 igralnih kock, ki so jih leta 1984 izkopali na bregu Temze. Bile so last profesionalnega goljufa s konca 15. stoletja. Od vseh kock jih je bilo 18 navrtanih in obteženih. 11 kock je imelo vdelane tri tanke žile živega srebra in so največkrat pokazale 5 ali 6 pik. Sedem kock je bilo obdelanih tako, da so najpogosteje pokazale 1 ali 2 piki. Od ostalih šestih kock so bile tri kocke dvojno označene s 4, 5 in 6 pikami (tako kocko so imenovali high man), ostale tri pa so bile dvojno označene z 1, 2 in 3 pikami (low man).
USTVARITE NOVO ZNANJE – SPOZNAJTE NAJBOLJ MODRE WEBINARJE
Aktualne izobraževalne teme v obliki krajših spletnih izobraževanj so že na voljo! Pridobite kompetence prihodnosti, znanja in veščine, ki pedagoškim in strokovnim delavcem omogočajo strokovno in osebno rast.
Anekdota ob kockanju
Najbolj razvpito razpravo o kockanju je leta 1654 sprožil francoski vitez in strastni hazarder Antoine Gombauld de Méré. Njegova posebnost je bila stava, da bo v štirih zaporednih metih kocke vsaj enkrat padla šestica. De Méré je pri tej stavi vztrajno dobival in kopičil bogastvo, dokler se ni stave naveličal in je spremenil pogoje igre.
Odtlej je stavil, da bosta dve kocki v 24 zaporednih metih obe vsaj enkrat pokazali 6 pik. Po spremembi so se stvari začele obračati na slabše in kazalo je, da ga je sreča povsem zapustila. V obupu se je s pismom obrnil na tedaj najbolj znanega francoskega matematika Blaisa Pascala, ki je s problemom seznanil tudi kolega Pierra de Fermata. Izračunala sta, da je bila verjetnost zmage v prvi stavi približno 0,52 oz. 52 %, v drugi stavi pa malo manj od polovice, zato je vitez na dolge roke oz. v mnogo igrah izgubljal. Pascal se je v pismu Fermatu ob viteza obregnil z besedami: »Je zelo inteligenten, vendar je slab matematik; to pa je, kot veste sami, velika pomanjkljivost.«
SLIKA 4: Blaise Pascal (1623–1662) in Pierre de Fermat (1601–1665)
Pascal in verjetnostni račun
Pascal in Fermat se nista ukvarjala le z računanjem verjetnosti zmage pri določenih stavah, ampak tudi s problemom delitve stave v primeru, da se igra iz kakršnegakoli razloga ni končala. S to nalogo so se že prej spopadali mnogi italijanski matematiki iz obdobja renesanse. Med njimi so bili Pacioli, Cardan in Tartaglio, vendar zadovoljive rešitve niso našli. Fermat je do rešitve skušal priti tako, da je preštel vse mogoče zaključke igre. Potem je ugotavljal, kateri od teh bi bili za posameznega igralca ugodni. Toda preračunavanje je z naraščajočim številom iger postalo zelo zamudno.
Pascal je ubral drugo pot. V Razpravi o aritmetičnem trikotniku (Traité du triangle arithmétique) je pojasnil povezavo med števili aritmetičnega (Pascalovega) trikotnika in rešitvijo zastavljenega problema.
Verjetnostni račun po Pascalovem trikotniku
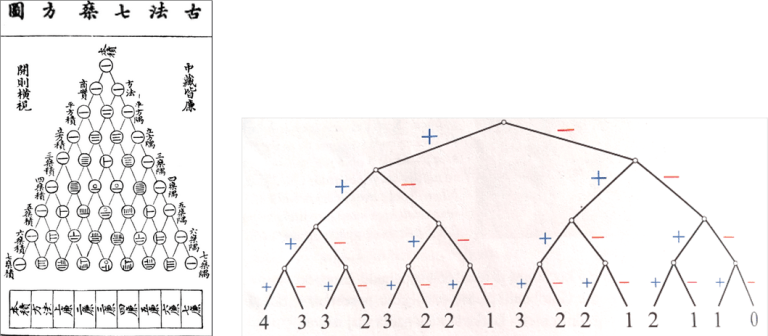
Recimo, da igralec A za končno zmago potrebuje dve igri, igralec B pa tri igre. Potem eden od obeh igralcev zagotovo zmaga v najmanj štirih igrah. Pogledamo 4. vrstico Pascalovega trikotnika: 1, 4, 6, 4, 1, in izračunamo razmerje, v katerem morata igralca deliti nagrado: (1 + 4 + 6) : (4 + 1) = 11 : 5. Razlaga je zelo preprosta, spada pa na področje kombinatorike.
Vseh mogočih izidov obeh igralcev pri štirih zaporednih igrah je 16. Iz kombinatoričnega drevesa je razvidno, da je od vseh možnosti le ena takšna, pri kateri A zmaga v štirih igrah, v štirih primerih zmaga trikrat, v šestih primerih dvakrat, v štirih primerih enkrat in v enem primeru vse štiri igre izgubi. Situacija za igralca B je ravno obrnjena. Od 16 možnih zaključkov je 11 zaključkov ugodnih za igralca A in 5 za igralca B, in zato morata dobitek razdeliti v razmerju 11 : 5.
SLIKA 5: Kitajski oz. Pascalov trikotnik, Kombinatorično drevo zadnjih štirih iger stave
Bernoulli in verjetnostni račun
V času Pascala in Fermata so v zvezi s srečo oz. dobitki govorili le o razmerjih števil in še niso uporabljali besede verjetnost. Prvi, ki je verjetnost dogodka umestil med števili 0 in 1, je bil Jacob Bernoulli. Napisal je razpravo o možnostih v igrah na srečo Ars Conjectandi, ki je izšla leta 1713, že po njegovi smrti. Posebno pomembna je bila njegova ugotovitev, da verjetnost dogodka lahko napovemo na podlagi njegove pogostosti v velikem številu ponovitev poskusa.
Bernoullijevo razpravo je za potrebe življenjskega zavarovanja prvi priredil protestantski begunec Abraham de Moivre, ki se je v Londonu preživljal z uradniškim delom.
Matematika, ki sta povzela de Moivrovo delo, sta bila britanska duhovnika in velika nasprotnika iger na srečo Thomas Bayes in Richard Price. Slednji je bil svetovalec za življenjsko zavarovanje pri družbi Equitable, ki je tedaj uspešno poslovala.
Verjetnostni račun v fiziki in astronomiji
Na prelomu stoletja je verjetnostni račun prek teorije napak, ki so jo razvili Adrien-Marie Legendre (1752–1833), Carl Friedrich Gauss (1777–1855) in Pierre Simone de Laplace (1749–1827), prodrl tudi v fiziko in astronomijo. Laplace je leta 1812 postavil prvo definicijo verjetnostnega računa, zato ga nekateri imenujejo tudi oče verjetnostnega računa.
Poseben pospešek je razvoju nove teorije dal angleški botanik Robert Brown, ki je leta 1828 opazil nepravilno gibanje semen v vodi. To, kar se danes imenuje Brownovo gibanje, so znanstveniki razumeli šele leta 1905, ko je Albert Einstein s svojimi raziskavami pojasnil molekularno gibanje kot naključni pojav.
Nadaljnji razvoj verjetnostne teorije smo v glavnem dolžni ruski matematični šoli, katere glavni predstavniki so Peter Lvovič Čebišev (1821–1894), njegov študent Andrej Andrejevič Markov (1856–1922) in Andrej Nikolajevič Kolmogorov (1903–1987). Slednji je v razpravi Temelji verjetnostne teorije leta 1933 postavil aksiome verjetnostnega računa.
Avtor prispevka: Gregor Pavlič