VRTENINE
Rotacija ali vrtenje je vsakodnevni pojav v življenju. In čeprav se nam pogosto vrti predvsem v glavi od vseh obveznosti ali zaradi navdušenja, v tem članku vrtenine spoznavamo kot matematični pojem.
Poleg številnih rotacij, ki jih opazimo (rotacijska luč na vozilih nujne vožnje, mlinsko kolo, vrtenje koles na vozilih …), je bistvena rotacija Zemlje, ki ni vidna, jo pa lahko občutimo. Njena najopaznejša posledica je menjavanje dneva in noči, vpliva pa tudi na plimovanje morja. V matematiki je zasuk ali vrtež ena osnovnih preslikav.
Vrtenine (rotacijska telesa) so geometrijska telesa, ki nastanejo z vrtenjem ravninskega geometrijskega lika okoli osi vrtenja. Tako nastalo telo je lahko tudi sestavljeno geometrijsko telo, katerega površina je enaka vsoti ploščin vseh mejnih ploskev, ki telo omejujejo, prostornina pa je enaka vsoti ali razliki posameznih prostornin.
Za lažje seznanjanje s pojmom vrtenine sem v nadaljevanju pripravila temeljito zbirko nalog, ki se jih lahko lotite s svojimi učenci.
Spoznavanje vrtenin
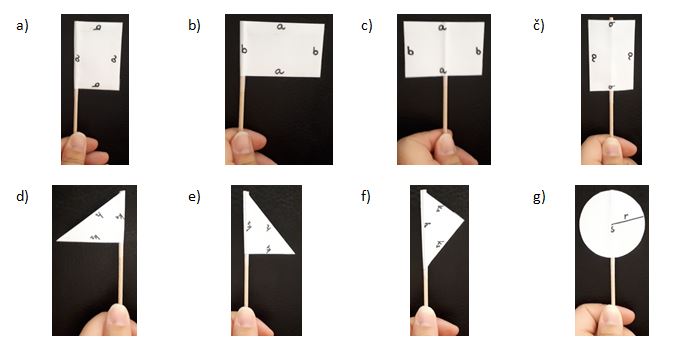
- Za lažjo vizualizacijo pojma naj učenci pri pouku izdelajo pripomoček: palčke z nalepljenimi liki. Iz papirja izrežejo 4 skladne pravokotnike, 3 skladne pravokotne trikotnike in en krog. Označijo jih, kot kaže slika.
Like nalepijo na palčke, kot kažejo fotografije.
Palčka ponazarja os vrtenja. Primi jo med prste in zavrti. Katero telo opiše lik med vrtenjem? Skiciraj ga in označi.
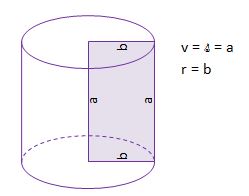
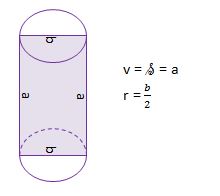
a) os vrtenja je nosilka stranice a – VALJ
b) os vrtenja je nosilka stranice b – VALJ
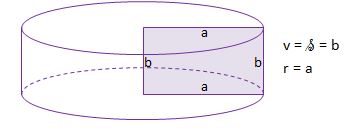
c) os vrtenja je simetrala stranice a – VALJ
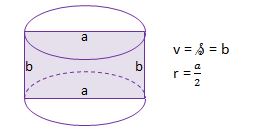
č) os vrtenja je simetrala stranice b – VALJ
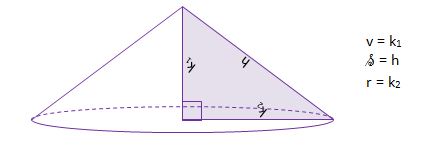
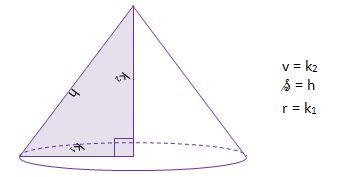
d) os vrtenja je nosilka katete k1 – STOŽEC
e) os vrtenja je nosilka katete k2 – STOŽEC
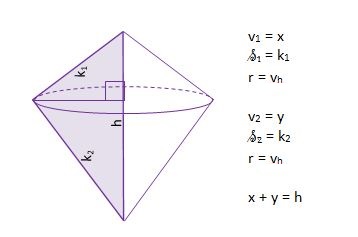
f) os vrtenja je nosilka hipotenuze – DVOJNI STOŽEC
g) os vrtenja je nosilka premera – KROGLA
VRTENINE: Računske naloge
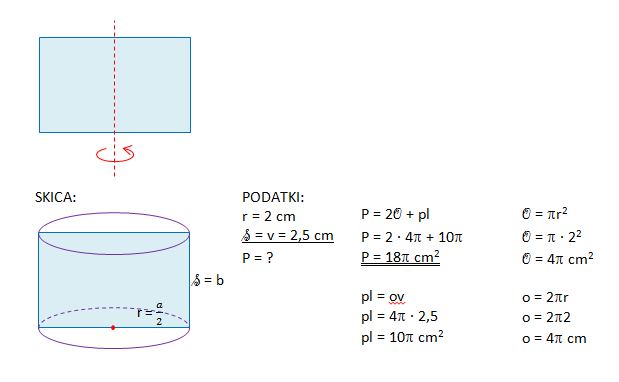
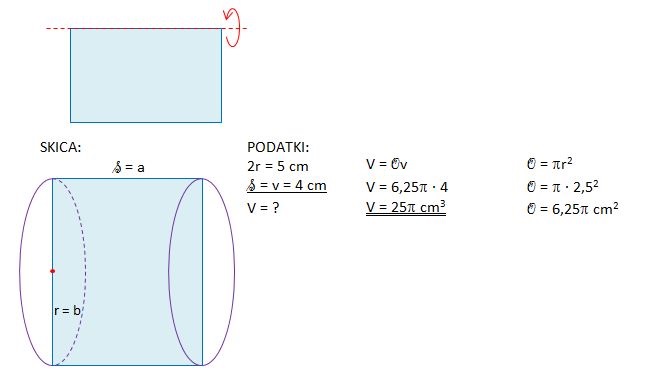
1. Ugotovi, katero telo nastane z vrtenjem pravokotnika z dimenzijami 4 cm x 2,5 cm okoli dane osi za polni kot, in ga skiciraj.
a) Tako nastalemu telesu določi polmer osnovne ploskve in višino ter izračunaj njegovo površino.
b) Tako nastalemu telesu določi premer osnovne ploskve in višino ter izračunaj njegovo prostornino.
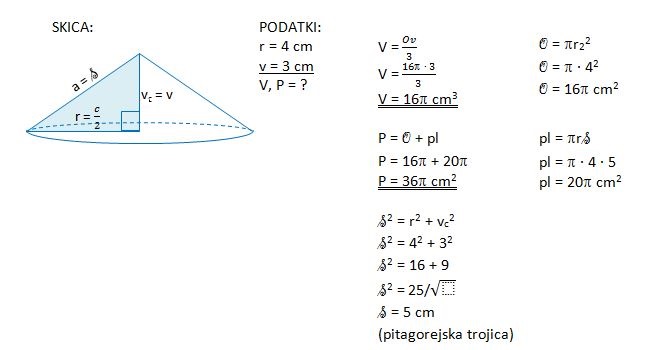
2. Pravokotni trikotnik s katetama 6 cm in 8 cm za 360° zavrtimo okoli hipotenuze. Nastaneta dva stožca, ki imata skupno osnovno ploskev s polmerom 4,8 cm. Skiciraj nastalo telo in izračunaj njegovo površino.
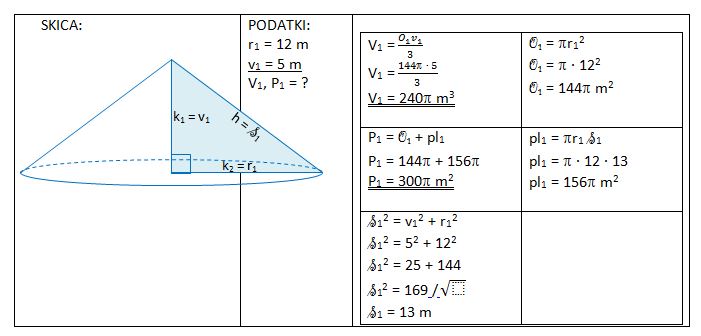
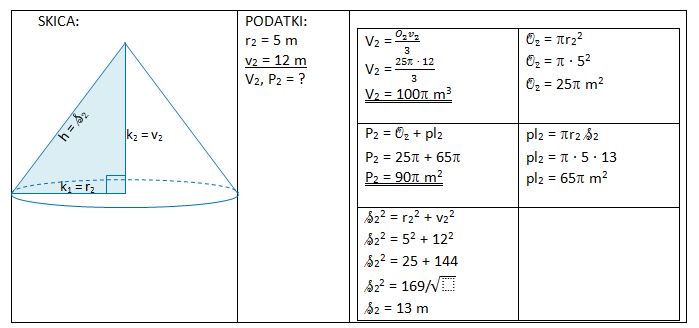
3. Pravokotni trikotnik s katetama 5 m in 12 m zavrtimo okoli katet za 360°. Nastaneta dva stožca. Skiciraj ju.
a) Za koliko se razlikujeta njuni prostornini?
b) Za koliko se razlikujeta njuni površini?
4. Kvadrat s ploščino 81 dm2 za 360° zavrtimo okoli nosilke stranice. Izračunaj površino in prostornino nastale vrtenine. Skiciraj jo.
5. Enakokraki trikotnik z osnovnico 8 cm in višino 3 cm za 180° zavrtimo okoli nosilke višine na osnovnico. Izračunaj prostornino in površino nastale vrtenine. Skiciraj jo.
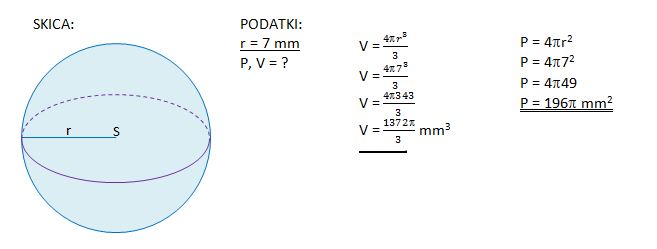
6. Krog s premerom 14 mm za 180° zavrtimo okoli nosilke premera. Izračunaj površino in prostornino nastale vrtenine. Skiciraj jo.
USTVARITE NOVO ZNANJE – SPOZNAJTE NAJBOLJ MODRE WEBINARJE
Aktualne izobraževalne teme v obliki krajših spletnih izobraževanj so že na voljo! Pridobite kompetence prihodnosti, znanja in veščine, ki pedagoškim in strokovnim delavcem omogočajo strokovno in osebno rast.
VRTENINE: Težje naloge
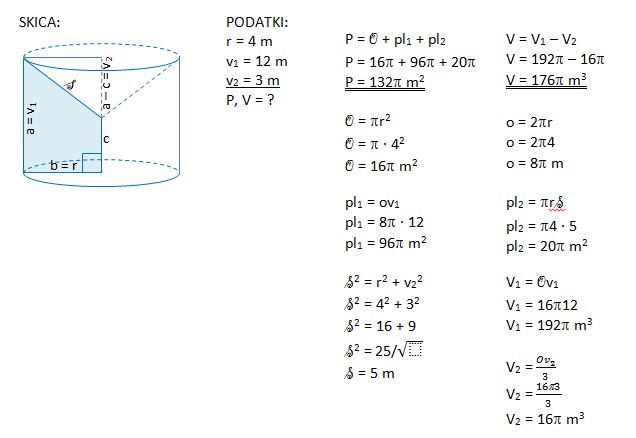
1. Pravokotni trapez z osnovnicama 6 cm in 9 cm ter višino 4 cm zavrtimo okoli kraka, ki je pravokoten na osnovnici za polni kot. Nariši skico ter izračunaj površino in prostornino nastale vrtenine.
2. Pravokotni trapez z osnovnicama 9 m in 12 m ter višino 4 m zavrtimo za polni kot okoli nosilk krajše osnovnice in daljše osnovnice, da nastaneta vrtenini. Nariši skici ter izračunaj njuni površini in prostornini.
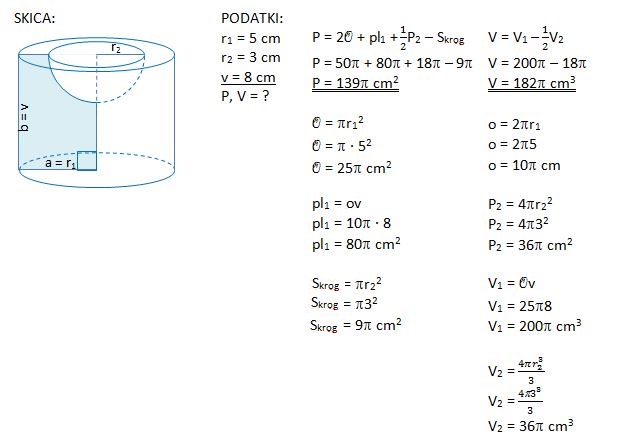
3. Iz pravokotnika z dolžino 5 cm in širino 8 cm izrežemo četrtino kroga s središčem v oglišču D in polmerom 3 cm. Dobljeni lik zavrtimo okoli nosilke daljice AD za polni kot. Nariši skico nastale vrtenine ter izračunaj njeno površino in prostornino.
Zaniminost: Toroid
Če krog za 360° zavrtimo okoli osi, ki je več kot za polmer oddaljena od središča kroga, nastane telo, ki ga imenujemo TOROID, ploskev, ki telo omejuje, pa je TORUS ali SVITEK.
Naloge so na voljo tudi znotraj delovnih zvezkov, tako da jih lahko uporabite pri delu v razredu.
Avtorica prispevka: Simona Zupan